Circumference and Area of a Circle Calculator

Our Circumference and Area of a Circle Calculator is the best tool for finding the Circumference and Area of a Circle. Simply enter the radius or diameter of the circle and click the "Calculate" button.

Have you ever wondered how to measure the distance around a circular object or the space it covers? Understanding the circumference and area of circles is essential in many real-life situations, from calculating the length of a bike wheel's tire to determining the size of a circular swimming pool.
These concepts might seem tricky at first, but once you grasp the formulas and learn how to apply them, you'll find them surprisingly simple and useful.

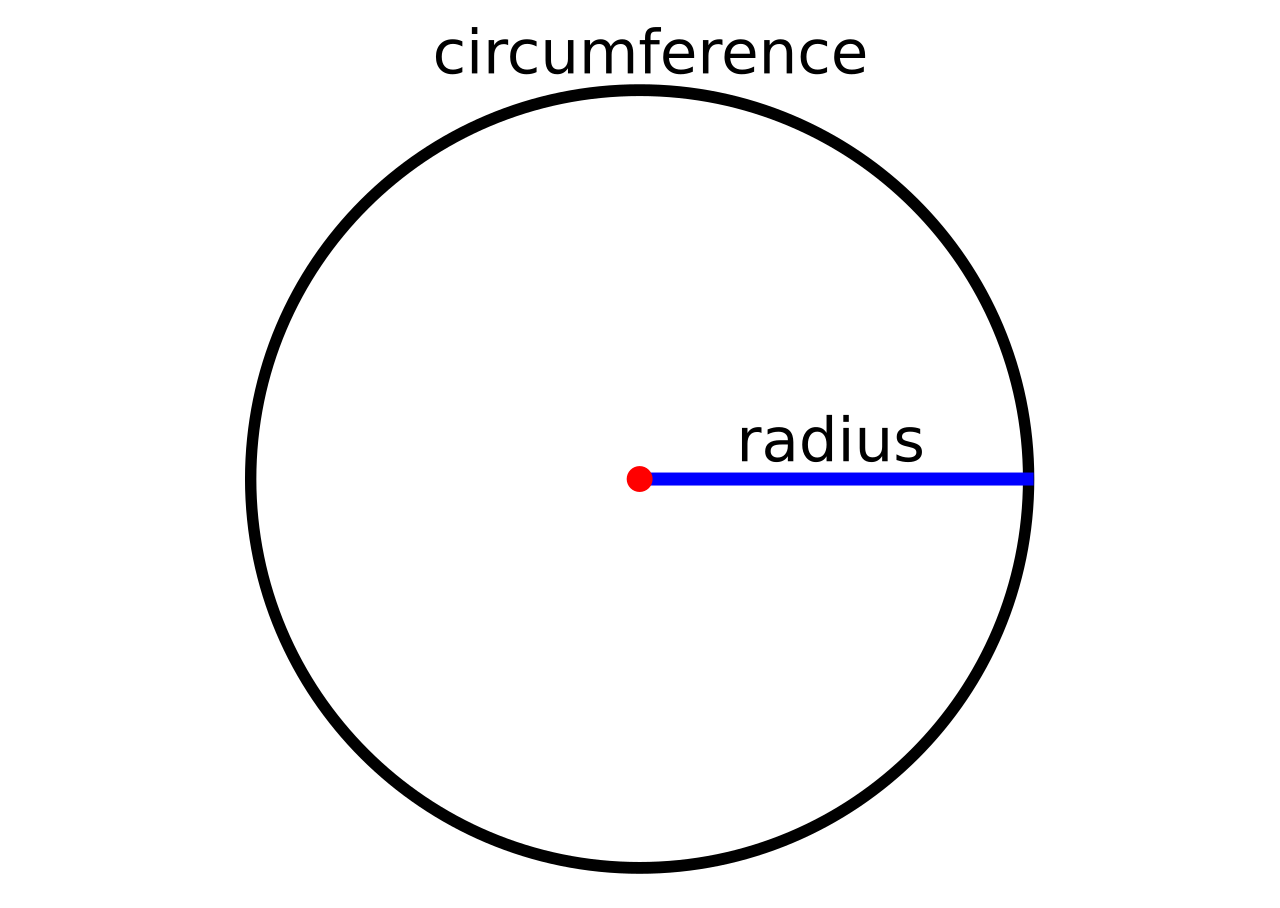
Formula to Calculate the Circumference and Area of a Circle

To calculate the circumference and area of a circle, we need to remember two important formulas:

Circumference formula: C = π × d (or C = 2 × π × r)
Area formula: A = π × r2

Let's break down these formulas and understand what each symbol represents:

• C stands for circumference, which is the distance around the circle.
• A stands for area, which is the space covered by the circle.
• π (pi) is a constant number with an approximate value of 3.14. It represents the ratio of a circle's circumference to its diameter.
• d stands for diameter, which is the length of a straight line passing through the center of the circle and connecting two points on the circle's edge.
• r stands for radius, which is the distance from the center of the circle to its edge.

How to Find the Circumference and Area of a Circle?

Now that we know the formulas and what each symbol means, let's learn how to find the circumference and area of a circle step-by-step.

Finding the Circumference:

1. Identify the diameter (d) or radius (r) of the circle.
2. If you know the diameter, substitute its value in the circumference formula: C = π × d.
   If you know the radius, substitute its value in the alternative circumference formula: C = 2 × π × r.
3. Perform the calculations and provide the final answer for the circumference.

Example: Suppose you have a circular coffee table with a diameter of 4 feet. To find its circumference, you would:
Circumference = π × d
Circumference = 3.14 × 4 feet
Circumference = 12.56 feet

Finding the Area:

1. Identify the radius (r) of the circle.
2. Substitute the value of the radius in the area formula: A = π × r2.
3. Perform the calculations and provide the final answer for the area.

Example: Let's say you want to know the area of a circular pizza with a radius of 8 inches. To find its area, you would:
Area = π × r²
Area = 3.14 × (8 inches)²
Area = 3.14 × 64 square inches
Area = 200.96 square inches

Frequently Asked Questions (FAQ)

What is the difference between circumference and area?

The circumference is the distance around the circle, while the area is the space covered by the circle. Circumference is a linear measurement (like feet or meters), and area is a square measurement (like square feet or square meters).

Why do we need to know the circumference and area of circles?

Understanding circumference and area of circles is essential in many real-life situations. For instance, knowing the circumference helps determine the length of a circular path or the amount of fencing required for a circular enclosure. Knowing the area helps calculate the size of a circular floor space, the amount of paint needed for a circular wall, or the size of a circular garden.

Can we find the circumference and area for an irregular shape?

No, the formulas for circumference and area only work for perfect circles. Irregular shapes have different methods for calculating their perimeter (distance around the shape) and area, depending on their specific shape.

What are some real-life applications of circumference and area of circles?

Real-life applications include calculating the length of a circular running track, determining the area of a circular dining table, finding the amount of wire needed for a circular wreath, and estimating the size of a circular pond or pool.

How can we remember the formulas for circumference and area?

Here are some memory aids:

• For circumference, think of the phrase "Circumference is Pi times Diameter" (C = π × d).
• For area, think of "Area is Pi times Radius Squared" (A = π × r2).
• Visualize a circle and remember that circumference is the distance around it, while area is the space it covers.

Conclusion

Understanding the circumference and area of circles might seem daunting at first, but with practice and familiarity with the formulas, it becomes straightforward. Remember, the circumference formula involves multiplying pi (π) by the diameter (d) or twice the radius (2 × r), while the area formula involves multiplying pi (π) by the radius squared (r2).

Applying these concepts in real-life situations will help you appreciate their importance and make calculations easier. Whether you're measuring a circular object, planning a landscaping project, or solving a geometry problem, mastering the circumference and area of circles will be a valuable skill.