Gradient Calculator of a Line
Result:
Our gradient calculator is the perfect tool for finding the gradient of a line from two points on that line. Our calculator shows the rise, run and gradient.
Have you ever wondered how steep a hill or ramp is? Or how to compare the steepness of different slopes? The gradient is a way to measure and describe how steep something is. In this article, we'll explore what the gradient is, how to calculate it, and why it's important.
What is the Gradient?
The gradient is a measure of how steep a slope is. It tells us how much something rises or falls for a certain horizontal distance. In other words, it's the "steepness" of a line or surface. A higher gradient means a steeper slope, while a lower gradient means a gentler slope.
For example, if you're looking at a wheelchair ramp, the gradient would tell you how steep the ramp is – a higher gradient means a steeper ramp that would be more difficult to navigate. Similarly, when hiking a trail, the gradient would indicate how strenuous the climb would be – a higher gradient means a steeper, more challenging hike.
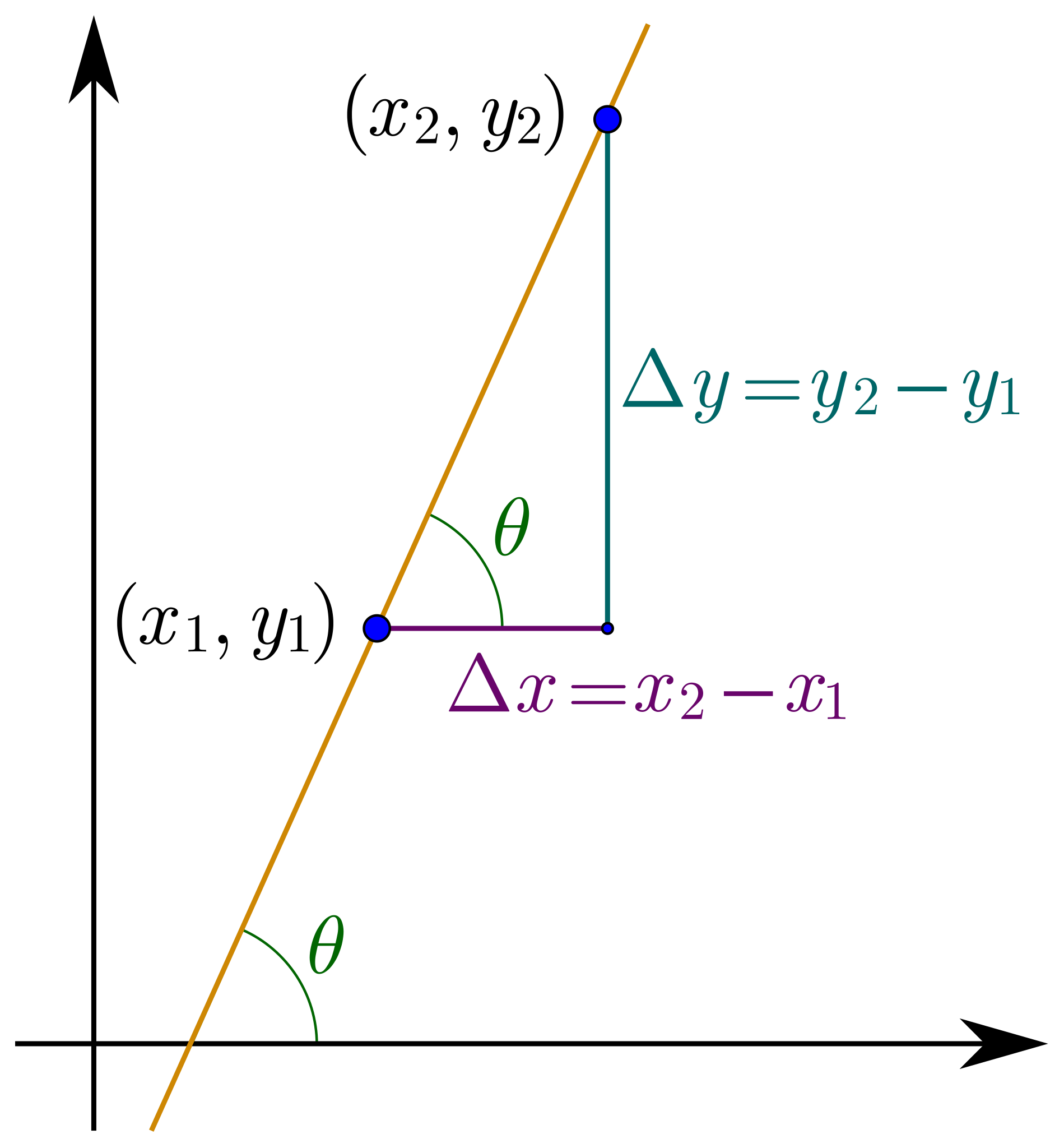
Gradient Definition
The formal definition of the gradient is the ratio of the vertical change (rise or fall) to the horizontal change (run) between two points on a line or surface. It's often represented by the symbol "m" in math.
For example, if a ramp rises 2 meters over a horizontal distance of 10 meters, the gradient would be 2/10 or 0.2.
Gradient Formula
The gradient formula is used to calculate the gradient between two points. Here's the formula:
gradient = rise / run
m = (y2 - y1) / (x2 - x1)
Let's break it down:
- m is the gradient (the value we want to find)
- y2 and y1 are the vertical coordinates (heights) of the two points
- x2 and x1 are the horizontal coordinates (distances) of the two points
To use the formula, you substitute the coordinate values of the two points and perform the calculation.
For example, if you have a line passing through the points (2, 3) and (6, 7), you can calculate the gradient as:
m = (7 - 3) / (6 - 2)
m = 4 / 4
m = 1
So the gradient of the line passing through those two points is 1.

How to Use This Gradient Calculator
A gradient calculator is a tool that can help you find the gradient between two points without having to do the math yourself. Here's how to use it:
- Go to the gradient calculator above.
- Enter the coordinates of the first point (x1, y1).
- Enter the coordinates of the second point (x2, y2).
- Press the "calculate" button (or equivalent).
- The calculator will display the gradient value (m).
It's that simple! The calculator does the work for you, so you don't have to worry about the formula or calculations.
For example, if you enter the coordinates (2, 3) and (6, 7) into the gradient calculator, it will calculate and display the gradient as 1, just like in the example above.
Understanding Gradient in Different Contexts
The concept of gradient extends beyond simple mathematical calculations and finds applications in numerous fields. Understanding these diverse applications helps appreciate the practical importance of gradient calculations in real-world scenarios.
Mathematical and Geometric Applications
In mathematics and geometry, gradient serves as a fundamental concept for understanding linear relationships:
Linear Equations and Functions
- Slope-Intercept Form: y = mx + b, where m represents the gradient
- Point-Slope Form: y - y₁ = m(x - x₁), utilizing gradient for line equations
- Rate of Change: Gradient represents constant rate of change in linear functions
- Proportional Relationships: Understanding direct and inverse proportionality through gradient
Coordinate Geometry
- Parallel Lines: Lines with identical gradients are parallel
- Perpendicular Lines: Lines with negative reciprocal gradients are perpendicular
- Distance and Midpoint: Gradient calculations support geometric analysis
- Area Calculations: Using gradient to find areas of geometric shapes
Engineering and Construction Applications
Engineers and construction professionals rely heavily on gradient calculations for designing safe and functional structures:
Civil Engineering Uses
- Road Design: Calculating appropriate gradients for vehicle safety and efficiency
- Drainage Systems: Ensuring proper water flow through gradient control
- Railway Construction: Designing grades that trains can safely navigate
- Pipeline Installation: Maintaining flow rates through proper gradient design
Accessibility and Safety Standards
- ADA Compliance: Ramps must have gradients no steeper than 1:12 (8.33%)
- Wheelchair Accessibility: Maximum gradient of 5% for comfortable navigation
- Emergency Egress: Stair gradients affecting evacuation safety
- Handrail Requirements: Gradient thresholds determining handrail necessity
Advanced Gradient Concepts
Different Ways to Express Gradient
Gradient can be expressed in various formats depending on the application and industry standards:
Numerical Expressions
- Decimal Form: 0.25 (rise of 1 unit per 4 units horizontal)
- Fraction Form: 1/4 (same relationship expressed as fraction)
- Percentage: 25% (decimal multiplied by 100)
- Ratio Form: 1:4 (vertical:horizontal relationship)
Angular Measurements
- Degrees: Converting gradient to angle using arctan function
- Radians: Alternative angular measurement system
- Grade Percentage: Engineering standard for expressing slope steepness
Gradient in Three-Dimensional Space
While basic gradient calculations involve two-dimensional coordinates, real-world applications often involve three-dimensional considerations:
Topographical Applications
- Contour Lines: Representing elevation changes through gradient analysis
- Terrain Modeling: Using gradients to model landscape features
- Watershed Analysis: Understanding water flow patterns through gradient mapping
- Erosion Prediction: Using gradient to predict soil erosion patterns
Practical Calculation Examples
Construction Project Example
Scenario: Designing a parking garage ramp
A parking garage needs a ramp connecting levels with a 12-foot height difference over a 144-foot horizontal distance.
Calculation:
- Rise = 12 feet
- Run = 144 feet
- Gradient = 12/144 = 0.083 = 8.3%
Analysis: This gradient meets typical parking garage standards (maximum 10%) and provides safe vehicle navigation.
Accessibility Ramp Example
Scenario: ADA-compliant ramp design
A building entrance is 30 inches above ground level and requires an ADA-compliant ramp.
Calculation:
- Maximum ADA gradient = 1:12 = 8.33%
- Required horizontal distance = 30 × 12 = 360 inches = 30 feet
- Actual gradient = 30/360 = 0.083 = 8.33%
Analysis: This design meets ADA requirements and ensures wheelchair accessibility.
Industry-Specific Gradient Standards
Transportation Infrastructure
Different transportation modes require specific gradient limitations for safety and efficiency:
Highway Design Standards
- Interstate Highways: Maximum 6% gradient in mountainous terrain
- Urban Streets: Typically limited to 8-12% depending on traffic volume
- Residential Roads: Maximum 10-15% with special design considerations
- Emergency Access: Fire department requirements may limit gradients to 10%
Railway Engineering
- High-Speed Rail: Maximum 3.5% gradient for safe operation
- Freight Railways: Typically limited to 2-3% for heavy loads
- Urban Transit: Metro systems may use gradients up to 6%
- Mountain Railways: Specialized systems may exceed 10% with safety measures
Building and Architecture
Stairway Design
- Residential Stairs: Rise/run ratio typically 7.5"/10" (75% gradient)
- Commercial Stairs: Maximum 7"/11" rise/run ratio (64% gradient)
- Public Buildings: ADA guidelines require specific rise/run relationships
- Emergency Stairs: Steeper gradients acceptable with proper safety features
Roof Design
- Flat Roofs: Minimum 1/4" per foot (2% gradient) for drainage
- Low-Slope Roofs: 1/4" to 3" per foot (2% to 25% gradient)
- Steep-Slope Roofs: Greater than 3" per foot (25% gradient)
- Snow Load Considerations: Steeper gradients reduce snow accumulation
Gradient in Natural Phenomena
Geological Applications
Understanding natural gradients helps in various geological and environmental studies:
River Systems
- Stream Gradient: Affects flow velocity and erosion patterns
- Flood Analysis: Gradient influences flood behavior and mitigation strategies
- Habitat Design: Fish ladders require specific gradients for species migration
- Hydroelectric Power: Gradient affects power generation potential
Landform Analysis
- Slope Stability: Steep gradients increase landslide risk
- Soil Erosion: Gradient affects soil loss rates and conservation needs
- Agriculture: Field gradient impacts irrigation and machinery operation
- Development Planning: Building restrictions based on slope gradients
Technology and Digital Applications
GPS and Navigation Systems
Modern technology incorporates gradient calculations for various applications:
Route Planning
- Vehicle Navigation: Avoiding steep gradients for fuel efficiency
- Bicycle Routing: Finding routes with appropriate gradients for cyclists
- Hiking Applications: Providing gradient information for trail difficulty assessment
- Accessibility Routing: Finding wheelchair-accessible routes with appropriate gradients
Engineering Software
- CAD Systems: Automated gradient calculation in design software
- GIS Applications: Terrain analysis and slope mapping
- Surveying Tools: Digital theodolites with gradient calculation capabilities
- Construction Apps: Mobile tools for field gradient verification
Other Similar Calculators
Check out other calculators that are similar to this one.
FAQs
To find the gradient between two points, follow these steps:
- Let's call the first point (x1, y1) and the second point (x2, y2).
- Calculate the rise by subtracting the y-values: y2 - y1.
- Calculate the run by subtracting the x-values: x2 - x1.
- To find the gradient, divide the rise by the run.
- You can also use an online gradient calculator to double-check your answer.
For example, if the first point is (2, 3) and the second point is (6, 7), the steps would be:
- The points are (2, 3) and (6, 7).
- The rise is 7 - 3 = 4.
- The run is 6 - 2 = 4.
- The gradient is 4 / 4 = 1.
- You can verify this gradient using our online calculator.
Remember, the gradient tells you how steep a line or slope is. A higher number means a steeper slope, and a lower number means a gentler slope.
The gradient is used in many different situations, such as:
- Measuring the steepness of hills, ramps, or slopes
- Comparing the steepness of different lines or surfaces
- Calculating the slope of a line in geometry or algebra
- Analyzing the rate of change in various scientific and engineering applications
For example, architects and engineers use gradients to design accessible ramps and structures, while construction workers need to understand gradients for building roads, railways, and other infrastructure.
The gradient itself is a unitless ratio or value. However, the vertical and horizontal units used in the calculation may vary depending on the situation. For example, if you're measuring the gradient of a ramp, the vertical unit might be meters (or feet), and the horizontal unit might be meters (or feet) as well.
Yes, the gradient can be negative. A negative gradient indicates that the line or slope is decreasing (going downwards) as you move from left to right.
For instance, if a road is sloping downhill, the gradient would be negative to represent the downward direction.
The gradient and slope are closely related concepts. In fact, the gradient is often referred to as the "slope" of a line. However, the term "slope" is more commonly used in geometry and algebra, while "gradient" is more commonly used in engineering and physics contexts.
The gradient is an important concept because it helps us understand and quantify the steepness of slopes, ramps, and other surfaces. This information is useful in various fields, such as construction, transportation, and accessibility planning. Understanding gradients can also help us solve mathematical and scientific problems involving rates of change or slopes.
For example, knowing the gradient of a wheelchair ramp is crucial for ensuring it meets accessibility standards and can be safely used by people with disabilities.
To convert gradient to percentage, multiply the decimal gradient by 100. For example, a gradient of 0.25 equals 25%. This percentage form is commonly used in engineering and construction to express slope steepness.
The maximum gradient for ADA-compliant ramps is 1:12 (8.33% or about 4.8 degrees). This means for every 1 inch of rise, there must be at least 12 inches of horizontal run to ensure wheelchair accessibility and safety.
Parallel lines have identical gradients - they never intersect because they rise at the same rate. Perpendicular lines have gradients that are negative reciprocals of each other. If one line has gradient m, the perpendicular line has gradient -1/m.
For driving, gradients above 10% (1:10) are generally considered steep. Highway standards typically limit gradients to 6% on interstates, while urban streets may allow up to 12%. Gradients above 15% require special considerations for vehicle safety and performance.
Find Calculator
Popular Calculators
Other Calculators
