Area of a Triangle Calculator - Find Triangle Area

Our Area of Triangle calculator is a quick and easy way to calculate the area of a given triangle using its Base and Height, Three Sides, Two Sides and Included Angle, or Two Angles and Included Side.

You've probably seen triangles all around you – in the shape of a slice of pizza, a roof on a house, or even the path that a ball takes when you kick it into the air. Triangles are one of the most common shapes in the world around us. But do you know how to calculate the area inside a triangle?

Knowing how to find the area of a triangle is an important skill that can be useful in many different situations. For example, if you want to cover a triangular garden bed with mulch or sod, you need to know its area so you can purchase the right amount of materials. If you're making a sail for a boat, the sail will likely be a triangular shape, and you'll need to calculate its area. There are lots of other cases where this comes in handy too!

How to Calculate the Area of a Triangle

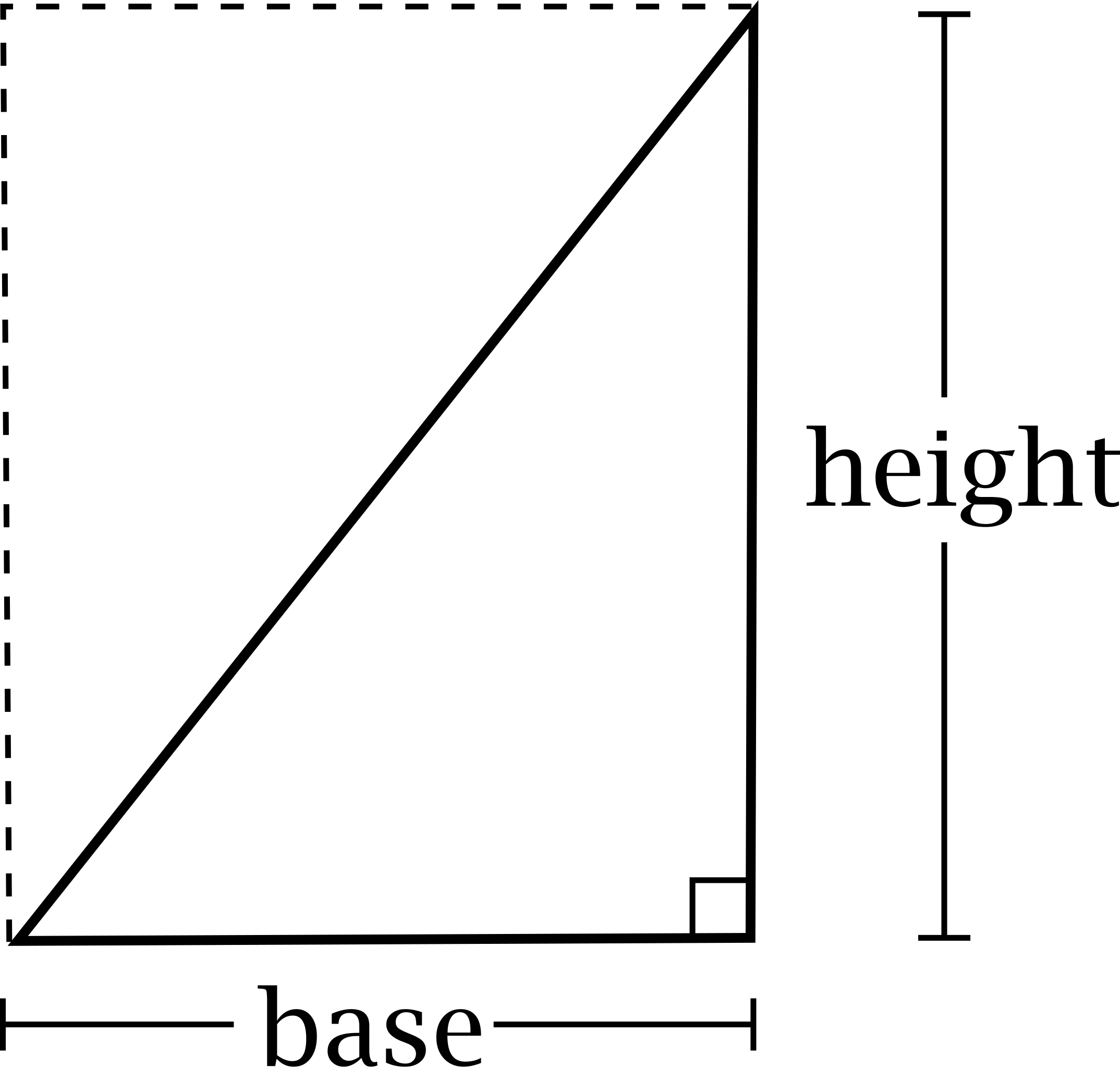
To calculate the area of any triangle, you need to know two key measurements – the base and the height.

The base of a triangle is simply the length of one of its sides. It can be any of the three sides.

The height is the shortest distance from the base to the opposite vertex (corner point) of the triangle. It forms a perpendicular (90 degree angle) with the base.

Here's an illustration to help visualize the base and height:

Once you know the base and height measurements, you're ready to use the formula to calculate the area.

The Formula for Calculating the Area of a Triangle

The most well-known and straightforward formula for calculating the area of a triangle is:

Area = 0.5 × base × height

Where:

• 0.5 means one-half
• base is the length of the base side of the triangle
• height is the perpendicular distance from the base to the opposite vertex (also called the altitude)

This formula gives you the area because a triangle's area is equal to one-half the area of a rectangle with the same base and height.

However, sometimes you may not have the height measurement. In those cases, there are other formulas you can use depending on what information you do have about the triangle:

Three Sides (SSS):
If you know the lengths of all three sides (a, b, c), you can use Heron's formula:

Area = 0.25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

Two Sides and Included Angle (SAS):
When you know two side lengths (a, b) and the angle between them (γ), the area can be calculated using:

Area = 0.5 × a × b × sin(γ)

Two Angles and Included Side (ASA):
If you know two angles (β, γ) and the side between them (a), you can use this formula:

Area = a2 × sin(β) × sin(γ) / (2 × sin(β + γ))

These alternative formulas allow you to find the area when you don't have the height, by utilizing other given information about the sides and angles.

Let's look at an example using the standard base × height formula:

Suppose a triangle has a base of 8 inches and a height of 6 inches.

Area = 0.5 × 8 in × 6 in
= 24 square inches

So by taking half of the base length (8 in) and multiplying it by the height (6 in), we get the area of 24 square inches.

The base × height formula is the most straightforward, but keep those alternative formulas in mind for cases when you don't have that specific information!

Equilateral Triangles

There's a special formula for finding the area of equilateral triangles. An equilateral triangle has all three sides equal in length.

The formula is:

Area = (√3/4) × side2

Where:

• √3 is the square root of 3 (approximately 1.73)
• side is the length of any of the three equal sides

For example, if each side of the equilateral triangle is 6 inches:

Area = (√3/4) × 62
= (1.73/4) × 36
= 0.433 × 36
= 15.6 square inches

This formula works because in an equilateral triangle, the height is always (√3/2) × side length.

Practice Problems

Okay, time to practice what you've learned so far! Try calculating the area for these triangles:

1) A triangle has a base of 8 cm and a height of 6 cm. What is its area?

To solve:
Area = 1/2 × base × height
= 1/2 × 8 cm × 6 cm
= 24 square cm

2) An equilateral triangle has sides of length 9 inches. Find its area.

Using the special equilateral formula:
Area = (√3/4) × side2
= (√3/4) × 92
= (1.73/4) × 81
= 34.6 square inches

3) A right triangle has a base of 5 feet and a height of 12 feet. Calculate its area.

Area = 1/2 × base × height
= 1/2 × 5 ft × 12 ft
= 30 square feet

See, not too hard! The key things to remember are:

• Identify the base and height
• Use the formula Area = 1/2 × base × height
• For equilateral triangles, use the special (√3/4) × side2 formula

FAQs

Can I use any two sides of the triangle to find the area?

No, you specifically need to know the base and the height corresponding to that base. Just knowing two random side lengths is not enough information.

What if I don't know the height?

Then you'll need to use one of the special formulas based on the other information you do know, like two sides and an angle, or all three sides

Do I have to use inches/feet/centimeters, or can I use any units?

You can use any units you like – inches, feet, centimeters, meters, etc. Just be sure to use the same units for both the base and height when calculating.

Why is the formula multiplied by 1/2?

Because a triangle is really half of a rectangle with the same base and height. So the formula gives the area of that half rectangle.