Gradient Calculator of a Line

Our gradient calculator is the perfect tool for finding the gradient of a line from two points on that line. Our calculator shows the rise, run and gradient.

Have you ever wondered how steep a hill or ramp is? Or how to compare the steepness of different slopes? The gradient is a way to measure and describe how steep something is. In this article, we'll explore what the gradient is, how to calculate it, and why it's important.

What is the Gradient?

The gradient is a measure of how steep a slope is. It tells us how much something rises or falls for a certain horizontal distance. In other words, it's the "steepness" of a line or surface. A higher gradient means a steeper slope, while a lower gradient means a gentler slope.

For example, if you're looking at a wheelchair ramp, the gradient would tell you how steep the ramp is – a higher gradient means a steeper ramp that would be more difficult to navigate. Similarly, when hiking a trail, the gradient would indicate how strenuous the climb would be – a higher gradient means a steeper, more challenging hike.

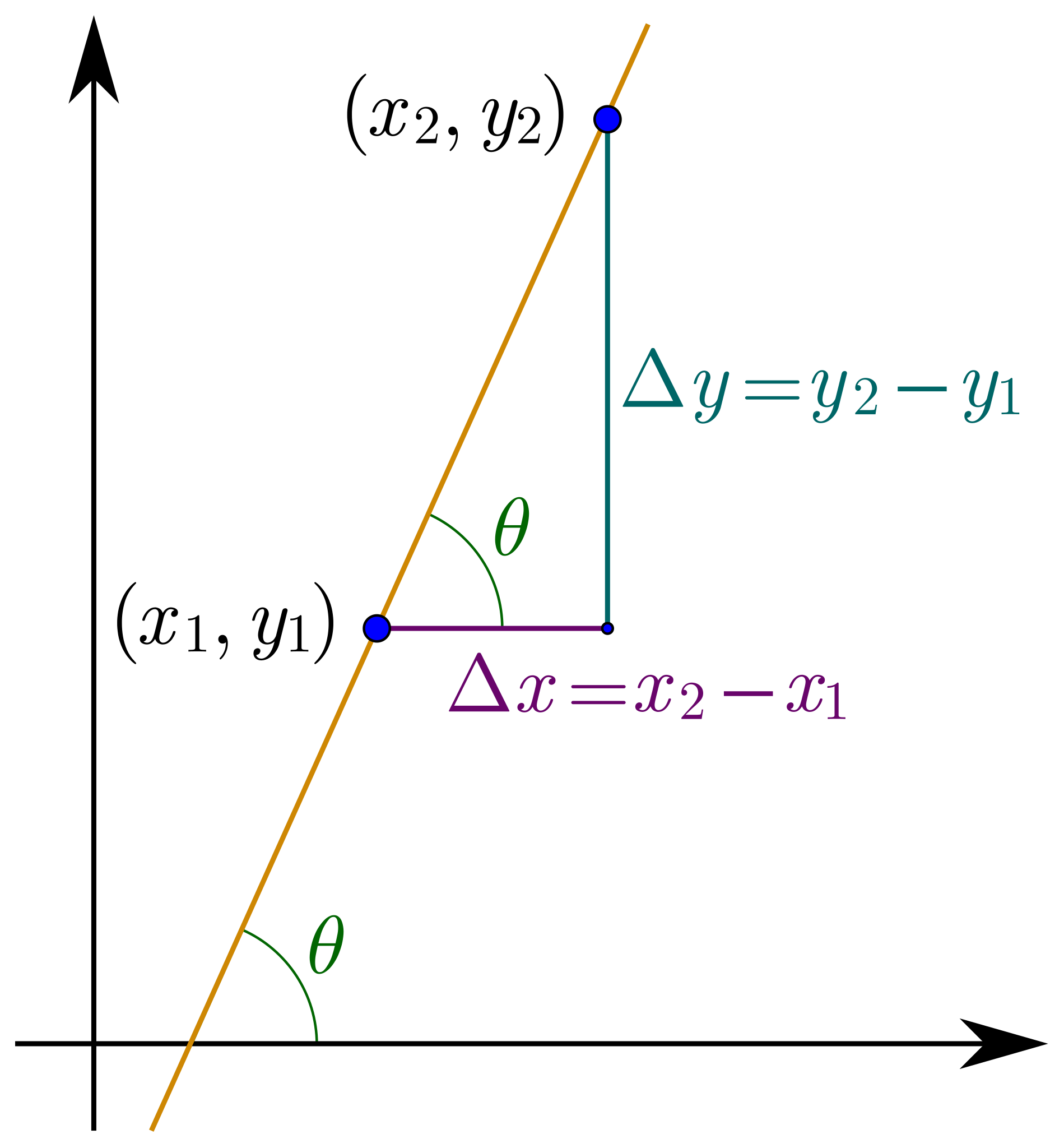
Gradient Definition

The formal definition of the gradient is the ratio of the vertical change (rise or fall) to the horizontal change (run) between two points on a line or surface. It's often represented by the symbol "m" in math.

For example, if a ramp rises 2 meters over a horizontal distance of 10 meters, the gradient would be 2/10 or 0.2.

Gradient Formula

The gradient formula is used to calculate the gradient between two points. Here's the formula:

gradient = rise / run

m = (y2 - y1) / (x2 - x1)

Let's break it down:

• m is the gradient (the value we want to find)
• y₂ and y₁ are the vertical coordinates (heights) of the two points
• x₂ and x₁ are the horizontal coordinates (distances) of the two points

To use the formula, you substitute the coordinate values of the two points and perform the calculation.

For example, if you have a line passing through the points (2, 3) and (6, 7), you can calculate the gradient as:

m = (7 - 3) / (6 - 2)
m = 4 / 4
m = 1

So the gradient of the line passing through those two points is 1.

How to Use This Gradient Calculator

A gradient calculator is a tool that can help you find the gradient between two points without having to do the math yourself. Here's how to use it:

1. Go to the gradient calculator above.
2. Enter the coordinates of the first point (x₁, y₁).
3. Enter the coordinates of the second point (x₂, y₂).
4. Press the "calculate" button (or equivalent).
5. The calculator will display the gradient value (m).

It's that simple! The calculator does the work for you, so you don't have to worry about the formula or calculations.

For example, if you enter the coordinates (2, 3) and (6, 7) into the gradient calculator, it will calculate and display the gradient as 1, just like in the example above.

FAQs

How do I calculate the gradient?

To find the gradient between two points, follow these steps:

1. Let's call the first point (x₁, y₁) and the second point (x₂, y₂).
2. Calculate the rise by subtracting the y-values: y₂ - y₁.
3. Calculate the run by subtracting the x-values: x₂ - x₁.
4. To find the gradient, divide the rise by the run.
5. You can also use an online gradient calculator to double-check your answer.

For example, if the first point is (2, 3) and the second point is (6, 7), the steps would be:

1. The points are (2, 3) and (6, 7).
2. The rise is 7 - 3 = 4.
3. The run is 6 - 2 = 4.
4. The gradient is 4 / 4 = 1.
5. You can verify this gradient using our online calculator.

Remember, the gradient tells you how steep a line or slope is. A higher number means a steeper slope, and a lower number means a gentler slope.

When is the gradient used?

The gradient is used in many different situations, such as:

• Measuring the steepness of hills, ramps, or slopes
• Comparing the steepness of different lines or surfaces
• Calculating the slope of a line in geometry or algebra
• Analyzing the rate of change in various scientific and engineering applications

For example, architects and engineers use gradients to design accessible ramps and structures, while construction workers need to understand gradients for building roads, railways, and other infrastructure.

What are the units of the gradient?

The gradient itself is a unitless ratio or value. However, the vertical and horizontal units used in the calculation may vary depending on the situation. For example, if you're measuring the gradient of a ramp, the vertical unit might be meters (or feet), and the horizontal unit might be meters (or feet) as well.

Can the gradient be negative?

Yes, the gradient can be negative. A negative gradient indicates that the line or slope is decreasing (going downwards) as you move from left to right.

For instance, if a road is sloping downhill, the gradient would be negative to represent the downward direction.

How does the gradient relate to slope?

The gradient and slope are closely related concepts. In fact, the gradient is often referred to as the "slope" of a line. However, the term "slope" is more commonly used in geometry and algebra, while "gradient" is more commonly used in engineering and physics contexts.

Why is the gradient important?

The gradient is an important concept because it helps us understand and quantify the steepness of slopes, ramps, and other surfaces. This information is useful in various fields, such as construction, transportation, and accessibility planning. Understanding gradients can also help us solve mathematical and scientific problems involving rates of change or slopes.

For example, knowing the gradient of a wheelchair ramp is crucial for ensuring it meets accessibility standards and can be safely used by people with disabilities.