Sector Area Calculator

Our Sector Area calculator is a handy tool for finding the sector area of a circle and determining its arc length. All you need to do is enter the central angle and radius of the circle and the calculator will do the rest.

What is a Sector of a Circle?

A sector of a circle is a portion of the circle's interior, cut off by two radii and the arc between them. It looks like a slice of pizza or a piece of pie. The two radii form the sides of the sector, and the curved part is called the arc.

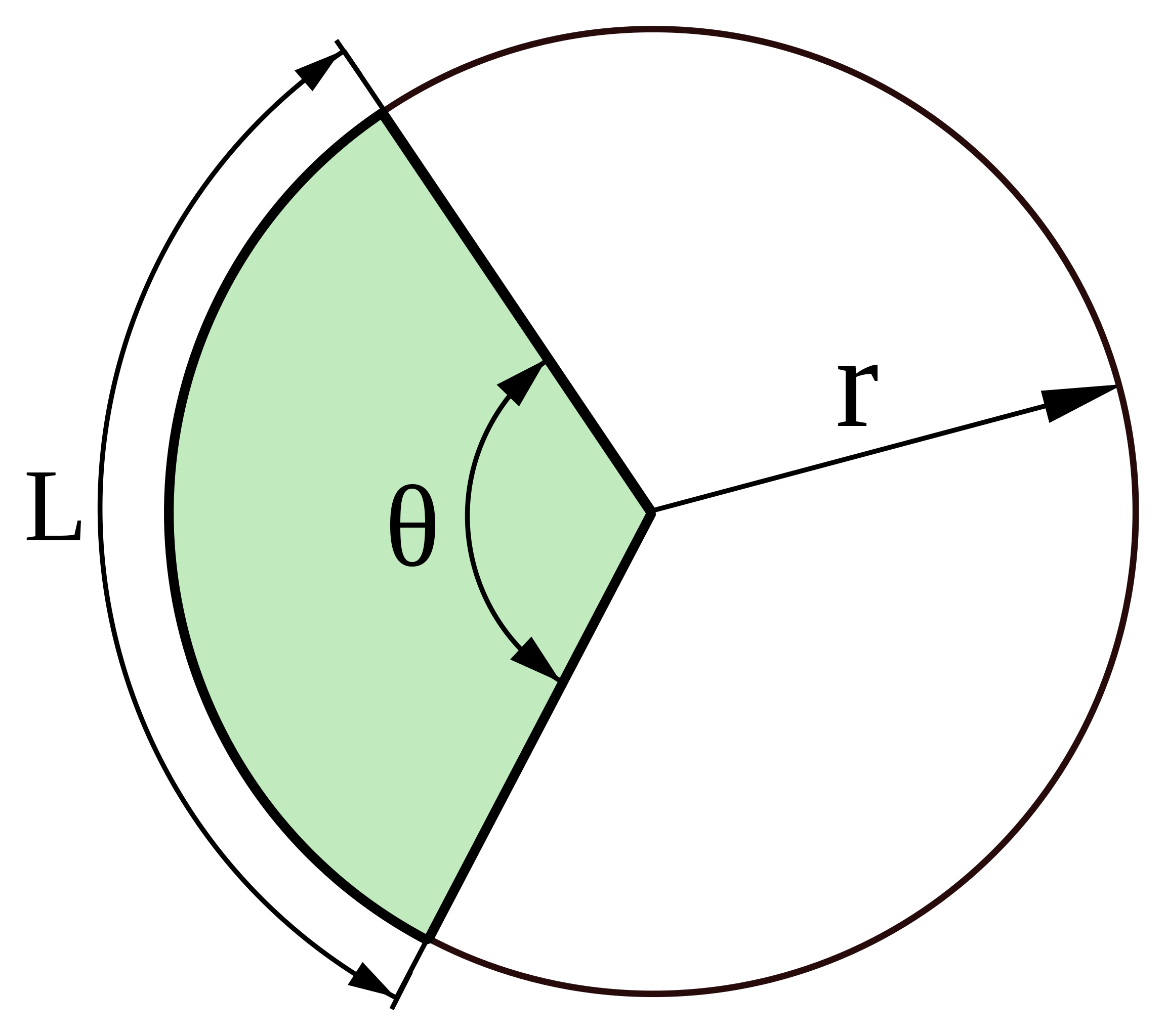
Key Parts of a Sector: To understand sectors better, let's look at the important parts:

• Central Angle: This is the angle formed by the two radii at the center of the circle. It determines how large the sector is.
• Arc Length: This is the length of the curved part of the sector.
• Radius: This is the distance from the center of the circle to its edge. The radius is the same for the whole circle.

Calculating the Area of a Sector

The Sector Area Formula: To find the area of a sector, we use a special formula:

Sector Area = (Radius)2 x (Central Angle in Radians) / 2

Let's break this down:

• Radius: This is the distance from the center to the edge of the circle. We square it because area is always calculated using the square of a length.
• Central Angle in Radians: Angles are measured in degrees or radians. For this formula, we need to use radians.
• Divide by 2: This part of the formula might seem strange, but it's necessary because the formula calculates the area of a whole circle. Since we only want the area of a sector (part of the circle), we divide by 2.

Step-by-Step Guide: To find the area of a sector, follow these steps:

1. Identify the radius (r) and the central angle (α) of the sector. The angle should be in radians.
2. Substitute these values into the formula: Sector Area = r2 x α / 2
3. Solve for the area by doing the calculations.

For example, let's find the area of a sector with a radius of 5 cm and a central angle of π/3 radians (60 degrees).

Step 1: r = 5 cm, α = π/3 radians
Step 2: Substitute into the formula:
Sector Area = (5 cm)2 x (π/3) / 2
= 25 cm2 x π/6
= 25 cm2 x 0.52 (approximately)
Step 3: Sector Area = 13 cm2

Special Cases

Area of a Semicircle: A semicircle is half of a circle. To find its area, we can use the sector area formula with a central angle of π radians (180 degrees). This gives:

Semicircle Area = r2 x π / 2 = πr2/2

For example, if the radius is 4 cm, the semicircle area is:

Semicircle Area = π(4 cm)2/2 = 32π/2 ≈ 25.13 cm2

Area of a Quadrant: A quadrant is one-fourth of a circle. Using the sector formula with a central angle of π/2 radians (90 degrees), we get:

Quadrant Area = r2 x (π/2) / 2 = πr2/4

If the radius is 6 inches, the quadrant area is:

Quadrant Area = π(6 in)2/4 = 108π/4 ≈ 21.21 in2

Sector Area Calculator - When Useful?

While you can calculate sector areas manually, sometimes it's helpful to use an online calculator tool, especially for:

• Large or complicated calculations with awkward numbers
• Checking your work if you're unsure about your answer
• Visualizing the sector and circle to better understand the concepts

FAQs

Can the sector area formula be used for any shape?

No, this formula only works for sectors of circles, not other shapes like rectangles or triangles.

What units are used for sector area?

Any area units can be used, like square centimeters (cm²), square inches (in²), etc. The units just have to match the units used for the radius.

How do I convert between angle units?

To convert from degrees to radians, multiply the degree value by π/180. To convert radians to degrees, divide the radian value by π/180.

What if I don't know the central angle?

If you know the arc length and radius, you can use the formula: Arc Length = r x Central Angle (in radians). Then solve for the central angle.

Can the sector area formula be used for sectors outside a circle?

No, this formula only applies to sectors inside a circle. For shapes outside circles, different area formulas are needed.

Conclusion

Understanding how to calculate the area of a sector is an important geometry skill. The key is knowing the sector area formula and being able to identify the radius and central angle. With examples and practice, you'll get better at visualizing sectors and finding their areas accurately. These formulas can then be extended to real-world applications in fields like architecture, engineering, and construction. So keep exploring sectors – you're learning valuable math concepts!